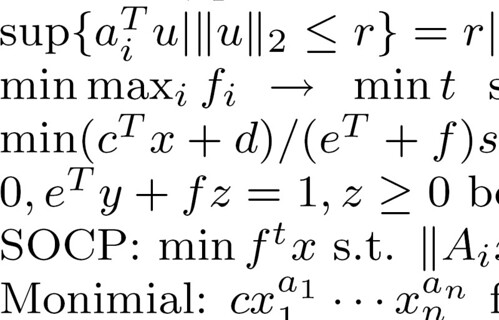In honor of the birthday of Ada Lovelace(1815-1852), founder of scientific computing, I am writing about Margaret Wright. She works with optimization which is both math and computing related, and helps solve practical problems, like when she was at Bell Labs, and had the task of how to set up an indoor wireless system at Home Depot. The stores are complicated in design, and optimization was a way to make a “good enough” system, that while not perfect, worked. I love her enthusiasm: “I don’t know if I can convey it without leaping up and down,” Wright exclaimed, “but there is such joy for mathematicians in helping to solve real world problems.” (Margaret Wright and Real World Mathematics)
In layman’s terms, the mathematical science of Convex Optimization is the study of how to make a good choice when confronted with conflicting requirements. The qualifier convex means: when an optimal solution is found, then it is guaranteed to be a best solution; there is no better choice.(Convex Optimization)
I like this idea that processes with uncertainty and many complications can be improved, even if they can’t be perfect, and I am fascinated that there are mathematical ways to figure out these improvements. (I suspect with the “Convex Optimization Cheat Sheet” below only works as a cheat sheet if you have some mathematical skill. . .)
How to Grow in a Math Job
Useful observations about growing in a job, and dealing with stereotypes in math and computing science, and would apply to other fields.
I can Wear a Math Hat and Computer Science Hat: An Interview with Margaret Wright
Wright mentions working with Nelder-Mead method, and I did a search in Flickr and found the cool photo above, with colors. Apparently, optimization can help with calibrating colors on different screens.
How Hard Can it Be? Lecture by Margaret Wright.
I understood much of the English parts of this, and nothing of the formulas, but it was an interesting discussion of cryptography among other practical problems.